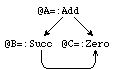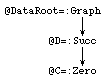|
|
The semantics of Clean is based on Term Graph Rewriting Systems (Barendregt, 1987; Plasmeijer and Van Eekelen, 1993). This means that functions in a Clean program semantically work on graphs instead of the usual terms. This enabled us to incorporate Clean’s typical features (definition of cyclic data structures, lazy copying, uniqueness typing) which would otherwise be very difficult to give a proper semantics for. However, in many cases the programmer does not need to be aware of the fact that he/she is manipulating graphs. Evaluation of a Clean program takes place in the same way as in other lazy functional languages. One of the “differences” between Clean and other functional languages is that when a variable occurs more than once in a function body, the semantics prescribe that the actual argument is shared (the semantics of most other languages do not prescribe this although it is common practice in any implementation of a functional language). Furthermore, one can label any expression to make the definition of cyclic structures possible. So, people familiar with other functional languages will have no problems writing Clean programs.
When larger applications are being written, or, when Clean is interfaced with the non-functional world, or, when efficiency counts, or, when one simply wants to have a good understanding of the language it is good to have some knowledge of the basic semantics of Clean which is based on term graph rewriting. In this chapter a short introduction into the basic semantics of Clean is given. An extensive treatment of the underlying semantics and the implementation techniques of Clean can be found in Plasmeijer and Van Eekelen (1993).
1.1 Graph Rewriting
A Clean program basically consists of a number of graph rewrite rules (function definitions) which specify how a given graph (the initial expression) has to be rewritten
A graph is a set of nodes. Each node has a defining node-identifier (the node-id). A node consists of a symbol and a (possibly empty) sequence of applied node-id’s (the arguments of the symbol) Applied node-id’s can be seen as references (arcs) to nodes in the graph, as such they have a direction: from the node in which the node-id is applied to the node of which the node-id is the defining identifier.
Each graph rewrite rule consists of a left-hand side graph (the pattern) and a right-hand side (rhs) consisting of a graph (the contractum) or just a single node-id (a redirection). In Clean rewrite rules are not comparing: the left-hand side (lhs) graph of a rule is a tree, i.e. each node identifier is applied only once, so there exists exactly one path from the root to a node of this graph.
A rewrite rule defines a (partial) function The function symbol is the root symbol of the left-hand side graph of the rule alternatives. All other symbols that appear in rewrite rules, are constructor symbols.
The program graph is the graph that is rewritten according to the rules. Initially, this program graph is fixed: it consists of a single node containing the symbol Start, so there is no need to specify this graph in the program explicitly. The part of the graph that matches the pattern of a certain rewrite rule is called a redex (reducible expression). A rewrite of a redex to its reduct can take place according to the right-hand side of the corresponding rewrite rule. If the right-hand side is a contractum then the rewrite consists of building this contractum and doing a redirection of the root of the redex to root of the right-hand side. Otherwise, only a redirection of the root of the redex to the single node-id specified on the right-hand side is performed. A redirection of a node-id n1 to a node-id n2 means that all applied occurrences of n1 are replaced by occurrences of n2 (which is in reality commonly implemented by overwriting n1 with n2).
A reduction strategy is a function that makes choices out of the available redexes. A reducer is a process that reduces redexes that are indicated by the strategy. The result of a reducer is reached as soon as the reduction strategy does not indicate redexes any more. A graph is in normal form if none of the patterns in the rules match any part of the graph. A graph is said to be in root normal form when the root of a graph is not the root of a redex and can never become the root of a redex. In general it is undecidable whether a graph is in root normal form.
A pattern partially matches a graph if firstly the symbol of the root of the pattern equals the symbol of the root of the graph and secondly in positions where symbols in the pattern are not syntactically equal to symbols in the graph, the corresponding sub-graph is a redex or the sub-graph itself is partially matching a rule. A graph is in strong root normal form if the graph does not partially match any rule. It is decidable whether or not a graph is in strong root normal form. A graph in strong root normal form does not partially match any rule, so it is also in root normal form.
The default reduction strategy used in Clean is the functional reduction strategy. Reducing graphs according to this strategy resembles very much the way execution proceeds in other lazy functional languages: in the standard lambda calculus semantics the functional strategy corresponds to normal order reduction. On graph rewrite rules the functional strategy proceeds as follows: if there are several rewrite rules for a particular function, the rules are tried in textual order; patterns are tested from left to right; evaluation to strong root normal form of arguments is forced when an actual argument is matched against a corresponding non-variable part of the pattern. A formal definition of this strategy can be found in (Toyama et al., 1991).
1.1.1 A Small Example
Consider the following Clean program:
Add Zero z = z (1)
Add (Succ a) z = Succ (Add a z) (2)
Start = Add (Succ o) o
where
o = Zero (3)
In Clean a distinction is between function definitions (graph rewriting rules) and graphs (constant definitions). A semantic equivalent definition of the program above is given below where this distinction is made explicit (“=>” indicates a rewrite rule whereas "=:" is used for a constant (sub-) graph definition
Add Zero z => z (1)
Add (Succ a) z => Succ (Add a z) (2)
Start => Add (Succ o) o
where
o =: Zero (3)
These rules are internally translated to a semantically equivalent set of rules in which the graph structure on both left-hand side as right-hand side of the rewrite rules has been made explicit by adding node-id’s. Using the set of rules with explicit node-id’s it will be easier to understand what the meaning is of the rules in the graph rewriting world.
x =: Add y z
y =: Zero => z (1)
x =: Add y z
y =: Succ a => m =: Succ n
n =: Add a z (2)
x =: Start => m =: Add n o
n =: Succ o
o =: Zero (3)
The fixed initial program graph that is in memory when a program starts is the following:
|
The initial graph in linear notation:
@DataRoot =: Graph @StartNode @StartNode =: Start
|
The initial graph in pictorial notation:
|
To distinguish the node-id’s appearing in the rewrite rules from the node-id’s appearing in the graph the latter always begin with a ‘@’.
The initial graph is rewritten until it is in normal form. Therefore a Clean program must at least contain a “ start rule” that matches this initial graph via a pattern. The right-hand side of the start rule specifies the actual computation. In this start rule in the left-hand side the symbol Start is used. However, the symbols Graph and Initial (see next Section) are internal, so they cannot actually be addressed in any rule.
The patterns in rewrite rules contain formal node-id’s. During the matching these formal nodeid’s are mapped to the actual node-id’s of the graph After that the following semantic actions are performed:
The start node is the only redex matching rule (3). The contractum can now be constructed:
|
The contractum in linear notation:
@A =: Add @B @C @B =: Succ @C @C =: Zero |
The contractum in pictorial notation:
|
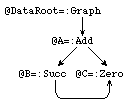
All applied occurrences of @StartNode will be replaced by occurrences of @A. The graph after rewriting is then:
|
The graph after rewriting:
@DataRoot =: Graph @A @StartNode =: Start @A =: Add @B @C @B =: Succ @C @C =: Zero |
Pictorial notation:
|
This completes one rewrite. All nodes that are not accessible from @DataRoot are garbage and not considered any more in the next rewrite steps. In an implementation once in a while garbage collection is performed in order to reclaim the memory space occupied by these garbage nodes. In this example the start node is not accessible from the data root node after the rewrite step and can be left out.
|
The graph after garbage collection:
@DataRoot =: Graph @A @A =: Add @B @C @B =: Succ @C @C =: Zero |
Pictorial notation :
|
The graph accessible from @DataRoot still contains a redex. It matches rule 2 yielding the expected normal form:
|
The final graph:
@DataRoot =: Graph @D @D =: Succ @C @C =: Zero |
Pictorial notation :
|
The fact that graphs are being used in Clean gives the programmer the ability to explicitly share terms or to create cyclic structures. In this way time and space efficiency can be obtained.
1.2 Global Graphs
Due to the presence of global graphs in Clean the initial graph in a specific Clean program is slightly different from the basic semantics. In a specific Clean program the initial graph is defined as:
@DataRoot =: Graph @StartNode @GlobId1 @GlobId2 … @GlobIdn
@StartNode =: Start
@GlobId1 =: Initial
@GlobId2 =: Initial
…
@GlobIdn =: Initial
The root of the initial graph will not only contain the node-id of the start node, the root of the graph to be rewritten, but it will also contain for each global graph (see 10.2) a reference to an initial node (initialized with the symbol Initial). All references to a specific global graph will be references to its initial node or, when it is rewritten, they will be references to its reduct.